suku banyak
Nomor 1

| Fungsi Invers Matematika Kelas 1 >Relasi Fungsi / Komposisi Fungsi-Fungsi Invers | 375 | ||
| f : A ® B Bila b Î B, maka invers dari elemen b (dinyatakan dengan f-1 (b)) adalah elemen A yang mempunyai pasangan b, atau f-1 (b) = {x ½ x Î A, f(x) = b} Jika f adalah fungsi dari A ® B, maka f mempunyai fungsi invers f-1 :A ® B jika dan hanya jika f adalah one one onto / bijektif / korespondensi 1-1
TEOREMA f : A ® B dan f-1 : B ® A f-1 o f : A ® A : fungsi indentitas di A f f-1 A ® B ® A (f-1 o f) f o f-1 : B ® B : fungsi identitas di B f-1 f B ® A ® B (f o f-1) | |||
Daftar isi[sembunyikan] |
 R terdefinisi pada garis bilangan riil, dan p, L
R terdefinisi pada garis bilangan riil, dan p, L  R maka kita menyebut limit f ketika x mendekati p adalah L, yang ditulis sebagai:
R maka kita menyebut limit f ketika x mendekati p adalah L, yang ditulis sebagai: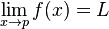

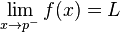
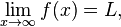
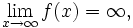
Daftar isi[sembunyikan] |

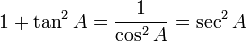
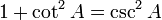

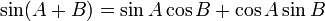

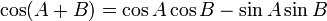



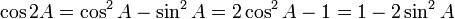




| I | II | III | IV | |
| a | + | - | - | + |
| b | + | + | - | - |
 cos x = cos a Þ x = ± a + n.360°
cos x = cos a Þ x = ± a + n.360°
 tg x = tg a Þ x = a + n.180° (n = bilangan bulat)
tg x = tg a Þ x = a + n.180° (n = bilangan bulat)

Daftar isi[sembunyikan] |

 adalah jari-jari lingkaran dan
adalah jari-jari lingkaran dan 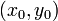 adalah koordinat pusat lingkaran.
adalah koordinat pusat lingkaran.

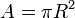


 dan jari-jari luar
dan jari-jari luar 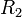 .
.

 dan jari-jari luar
dan jari-jari luar 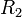 , yaitu
, yaitu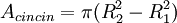
 rumus ini kembali menjadi rumus luas lingkaran.
rumus ini kembali menjadi rumus luas lingkaran.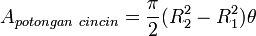
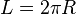
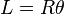
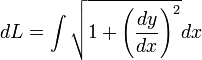
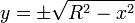
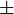 mengisyaratkan bahwa terdapat dua buah kurva, yaitu bagian atas dan bagian bawah. Keduanya identik (ingat definisi lingkaran), sehingga sebenarnya hanya perlu dihitung sekali dan hasilnya dikalikan dua.
mengisyaratkan bahwa terdapat dua buah kurva, yaitu bagian atas dan bagian bawah. Keduanya identik (ingat definisi lingkaran), sehingga sebenarnya hanya perlu dihitung sekali dan hasilnya dikalikan dua.